Chuyên đề Hệ số bất định lớp 8 Nâng cao – áp dụng vào thực hành làm các dạng bài quen thuộc. Đây là một phương pháp cực kỳ hay được áp dụng trong các bài toán về tính số trị của biểu thức, hay đi tìm các hằng số a b c để biểu thức A bằng biểu thức B… Chúng ta cùng đi tìm hiểu chi tiết về dạng toán này.
Dành cho các em chưa xem các tiết về rút gọn biểu thức:
Tiết 1: Rút Gọn Biểu Thức Lớp 8 – Tiết 1
Tiết 2: Rút Gọn Biểu Thức Lớp 8 – Tiết_2
Hệ số bất định là gì? Hệ số thì chúng ta biết rồi, trong biểu thức chúng ta có các phần là [phần hệ số][phần biến]. Ví dụ như 5x thì hệ số là 5 và biến số là x. Bất định là gì, bất định là chưa xác định được. Vậy Hệ số bất định hiểu nôm na là phần hệ số chưa xác định. Vậy làm sao để chúng ta có thể xác định được phần hệ số này, thì dạng toán hệ số bất định này luôn đi kèm với dạng toán “Đồng nhất đathức”. Có thể hiểu như sau, đa thức A bằng đa thức B khi các hệ số cùng bậc của đa thức A bằng các hệ số cùng bậc của đa thức B.
Ví dụ sau khi phân tích 1 bài tìm a,b chúng ta được: 5x + 6y = (1-a)x + (b+2)y
Thì (1-a) và (b+2) ở đây đóng vai trò như các hệ số bất định. Chúng ta đi đồng nhất đa thức thì:
5x = (1-a)x và 6y = (b+2)y Hay 5 = 1- a và 6 = b+2.
Đó chỉ là một ví dụ đơn giản để hiểu khái niệm về hệ số bất định, giờ chúng ta sẽ đi áp dụng vào xem các bài toán thực tế sẽ có dạng như nào nhé:
1. dạng toán phương pháp hệ số bất định lớp 8 nâng cao
2. Tiết số 1
3. Thời lượng: 30 phút
4. Số lượng bài: 7 bài
5. Mức độ: Khá – Giỏi
Cấu trúc tiết học:
1. Danh sách các bài sẽ học
2. Hướng dẫn và đáp án
3. Tổng kết tiết học
1. Danh sách 7 bài toán về hệ số bất định

2. Hướng dẫn giải chi tiết và đáp án



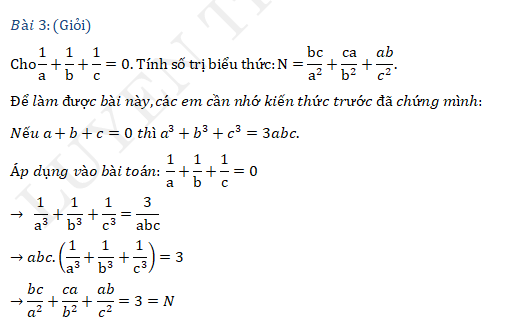




3. Tổng kết nội dung
Trong phần đầu áp dụng phương pháp hệ số bất định trong chương trình toán lớp 8 này, các em đã được học lý thuyết và thực hành về các bài toán hay gặp nhất, hướng dẫn cách giải chi tiết và đáp án của các bài. Sẽ còn rất nhiều các bài toán mà các em sẽ cần sử dụng phương pháp này, hãy xem các tiết tiếp theo về dạng toán hệ số bất định nâng cao trên Luyện Thi Nhanh nhé.
