Chuyên đề Các Dạng toán phương trình ax + b = 0 lớp 8 nâng cao. Dạng toán về phương trình liên quan tới ax + b rất đa dạng và biến đổi cực kỳ linh hoạt. Đây sẽ là một dạng toán hay với các em yêu thích môn Toán, vì tính chất của các bài toán liên quan tới Phương Trình thường kết hợp và áp dụng vào rất nhiều các kiến thức toán khác. Trong tiết đầu tiên, chúng ta sẽ đi tìm hiểu một chút về khái niệm sẽ được sử dụng trong quá trình học và áp dụng thực hành làm bài.
Chuyên đề về Các dạng toán phương trình ax + b = 0 chúng ta sẽ được học:
PHẦN I: LÝ THUYẾT
- Tiết 1. Lý thuyết Các dạng toán phương trình ax + b=0 lớp 8 nâng cao
- Tiết 2. Giải phương trình chưa ẩn số ở tử.
- Tiết 3. Phương trình chứa ẩn số ở mẫu thức.
- Tiết 4. Phương trình có chứa dấu giá trị tuyệt đối
- Tiết 5. Phương trình có chưa tham số.
- Tiết 6. Phương trình bậc cao.
- Tiết 7. Các dạng bài toán tổng hợp.
PHẦN II: THỰC HÀNH – Áp dụng các cách giải ở các tiết học để thực hành giải các dạng bài toán trong đề thi nâng cao.
I. KIẾN THỨC CƠ BẢN CẦN NHỚ
Cho phương trình f(x)= g(x). Nghiệm của phương trình xét trên tập A là số α∈A sao cho f(α)= g(α).
Tập A ở đây có thể là:
– Tập các số tự nhiên (N);
– Tập các số tự nhiên khác 0 (N*)
– Tập các số nguyên (Z);
– Tập các số hữu tỉ (Q);
– Tập các số vô tỉ (I);
Ví dụ: cho phương trình 2x+1=0 trên tập N.
Phương trình này sẽ vô nghiệm vì 2x+1 nhỏ nhất bằng 1 khi x=0;
Nhưng cho phương trình 2x+1=0 trên tập Z thì sao? Phương trình này sẽ có nghiệm x= 1/2 thoả mãn điều kiện.
Vậy việc giải phương trình f(x)=g(x) là tìm mọi giá trị của x để các giá trị tương ứng của hai biểu thức f(x) và g(x) bằng nhau. Tập hợp các giá trị làm cho f(x)= g(x) thì được gọi là tập nghiệm của phương trình, và sẽ được ký hiệu là S;
Còn phương trình dạng ax + b = 0 được gọi là phương trình bậc nhất; Bậc nhất ở đây có nghĩa là bậc của x lớn nhất trong nhiểu thức là bằng 1; sau nay chúng ta sẽ còn học lên các phương trình bậc 2; bậc 3 v.v…
Phương trình bậc nhất có nhiều nhất là 1 nghiệm.
II. THẾ NÀO LÀ HAI PHƯƠNG TRÌNH TƯƠNG ĐƯƠNG.
hai phương trình (1) và (2) gọi là tương đương trên tập A nếu tập nghiệm của (1) và (2) như nhau trong A (Kể cả trường hợp (1) và (2) cùng vô nghiệm trong A ).
Ví dụ xét tính tương đương của hai phương trình sau:
Phương trình 1: x^2 – 1 = 0
Phương trình 2: x – 1 = 0
a) Trên tập số tự nhiên N
b) Trên tập số nguyên Z
Chúng ta thấy 2 phương trình (1) và (2) trên tập số tự nhiên đều có duy nhất 1 nghiệm là x=1
→ hai phương trình là tương đương nhau: Viết là: x^2-1=0 ↔ x-1=0
Nhưng trên tập số nguyên thì phương trình 1 có 2 nghiệm là {-1;1} Vì vậy 2 phương trình sẽ là không tương đương với nhau.
III. PHÉP BIẾN ĐỔI TƯƠNG ĐƯƠNG.
Các phép biến đổi phương trình mà không làm thay đổi tập nghiệm của phương trình đó được gọi là các phép biển đổi tương đương.
Một số cách biến đổi tương đương thường sử dụng: 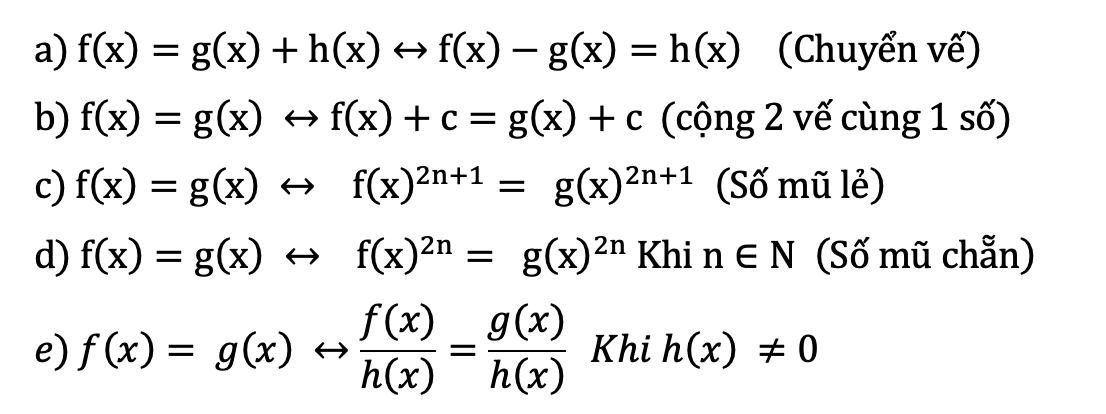
Trên đây là các cách và ví dụ thường gặp,trong mỗi điều kiện bài toán,chúng sẽ áp dụng linh hoạt các cách trên. Phần này sẽ được nhắc thêm trong các bài thực hành.

CÁC DẠNG BÀI TOÁN VỚI PHƯƠNG TRÌNH BẬC NHẤT 1 ẨN.
Dạng 1. Giải phương trình chưa ẩn số ở tử.
Dạng 2. Phương trình chứa ẩn số ở mẫu thức.
Dạng 3. Phương trình có chứa dấu giá trị tuyệt đối
Dạng 4. Phương trình có chưa tham số.
Dạng 5. Phương trình bậc cao.
Dạng 6. Các dạng bài toán tổng hợp.
Chúng ta sẽ tìm hiểu cách giải từng dạng thông qua các bài toán cụ thể từ cơ bản tới nâng cao trong chuyên đề này. Click lựa chọn dạng toán mà các em quan tâm!
